目录
目录
概述
在线工作坊 | 机器学习模型简介_哔哩哔哩_bilibili
人工智能, 机器学习, 深度学习的关系
人工智能(AI)是一种让计算机能够模仿人类智能的技术. 它包括机器学习;
- 机器学习(ML)是人工智能的一部分,它包括让计算机能够依靠经验更好地处理任务的多项技术(例如深度学习)
- 深度学习(DL) 又是机器学习的一部分,它以人工神经网络为基础,让计算机能够自我训练
- 机器学习(ML)是人工智能的一部分,它包括让计算机能够依靠经验更好地处理任务的多项技术(例如深度学习)
传统编程与机器学习
传统编程
机器学习
机器学习的一般步骤
数据建模需要的只是最多,基本上由有经验的硕士/博士处理
机器学习环境和基本库介绍
- numpy, scikit-learn, matplotlib, pandas, jupyter
- scikit-learn(简称sklearn),是用 python 实现的机器学习算法库。sklearn 可以实现数据预处理、分类、回归、降维、模型选择等常用的机器学习算法。sklearn 是基于 Numpy, Scipy, matplotlib 的。
- 简单高效的数据挖掘和数据分析工具
- 可供各种环境中重复使用
- 建立在 Numpy, Scipy 和 matplotlib 上
- 开源, 可商业使用 - BSD 许可证
环境搭建
WSL2
Tensorflow with DirectML on WSL 2 | Microsoft Docs
使用 Python 探索和分析数据
- 随笔基于 Microsoft Learn: 使用 Python 探索和分析数据 - Learn | Microsoft Docs
简介
- 简介 - Learn | Microsoft Docs
- 毫不奇怪的是,数据科学家这一角色主要是探索和分析数据。 这种分析的结果可能是为报表或机器学习模型奠定基础;但这一切都始于数据。
机器学习是处理预测建模的数据科学的一个子集。 换言之,就是使用数据创建可预测未知值的模型。 它的工作原理是识别描述某物特性的数据值(特征) 和我们想要预测的值(标签) 之间的关系,并通过训练过程将这些关系封装在模型中。
Exercise - Explore data with NumPy and Pandas
- List 不支持科学计算, 用 List 数据生成 Numpy.array 数据就可以支持科学计算了
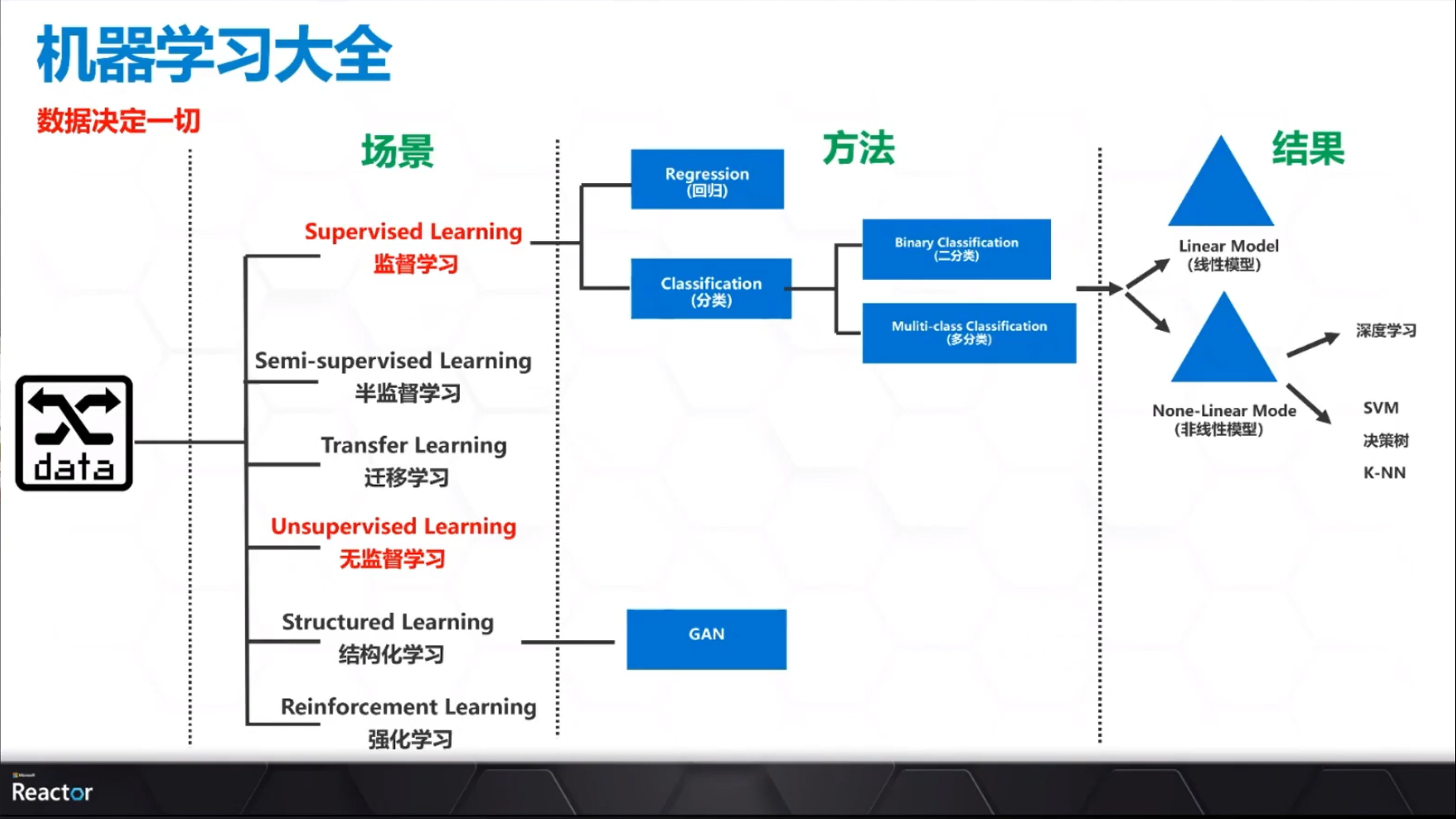
监督学习简介
- Supervised Learning
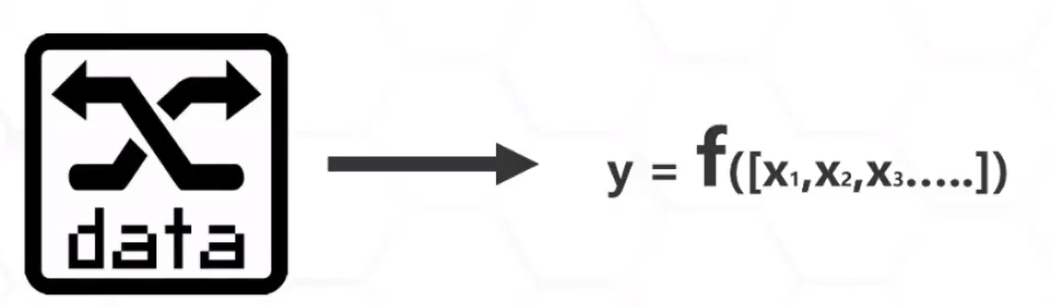
经验决定一切,整合大量的标注数据,应用在预测价格,[判断分类等场景上
需要找到一个基于特征数据,生成结果的方法
一般都有多个特征数据
x 值拟合到计算中, 从而为训练数据集中的所有情况合理准确地生成 y
监督学习的常见解决方法
Regression(回归)[预测明天的气温是多少度] Classification(分类)[预测明天是阴\晴还是雨] 输出 连续数据 离散数据 目的 定量-找到最佳拟合 定性-决策边界 评价 拟合度 精度 场景 预测房价,天气 垃圾邮件,物品分类
训练和评估回归模型
随笔基于 Microsoft Learn: 简介 - Learn | Microsoft Docs
部分内容为通篇摘抄, 含适当改动与注释
回归是机器学习的一种形式,其目标是创建一个可预测数值、可计量值的模型,例如价格、金额、大小或其他标量数字。
例如,一家出租自行车的公司可能希望根据季节、星期几、天气情况等来预测给定某天的预期租赁数。
回归的工作原理是在表示被观察的事物特征(称为特征) 的数据变量与我们试图预测的变量(称为标签) 之间建立关系。 在本例中,我们观察有关日子的信息,因此特征包括星期几、月份、温度、降雨量等。而标签是自行车租赁数。
为了训练模型,我们从包含特征和标签已知值的数据样本开始,因此,在此例中,我们需要包含日期、天气情况和自行车租赁数的历史数据。 然后,将此数据样本拆分为两个子集:
- 训练数据集,我们将对其应用一种算法,该算法确定封装了特征值与已知标签值之间关系的函数。
- 验证或测试数据集,可用来评估模型,方法是使用该数据集生成标签的预测,并将预测与实际的已知标签值进行比较。
使用具有已知标签值的历史数据来训练模型使回归成为监督式机器学习的一个示例。
一个简单示例
让我们通过一个简单的示例来了解训练和评估过程的原理。 假设我们简化了方案,以便可以使用单个特征(即每日平均温度) 来预测自行车租赁标签。
我们从一些数据开始,其中包括每日平均温度特征和自行车租赁标签的已知值。
| 温度 | 租赁数 |
|---|---|
| 56 | 115 |
| 61 | 126 |
| 67 | 137 |
| 72 | 140 |
| 76 | 152 |
| 82 | 156 |
| 54 | 114 |
| 62 | 129 |
现在,我们将采用这些观察值中的前五个,并使用它们来训练回归模型(在实际情况中,是将数据随机拆分为训练和验证数据集。重要的是,拆分必须是随机的,以确保每个子集在统计上是相似的) 。 训练模型的目标是要找到一个可以应用于温度特征(可称之为 x) 的函数(可称之为 f) ,以计算租赁标签(可称之为 y) 。 换句话说,我们需要定义以下函数:f(x) = y。 训练数据集如下所示:
首先,在图表上绘制 x 和 y 的训练值:
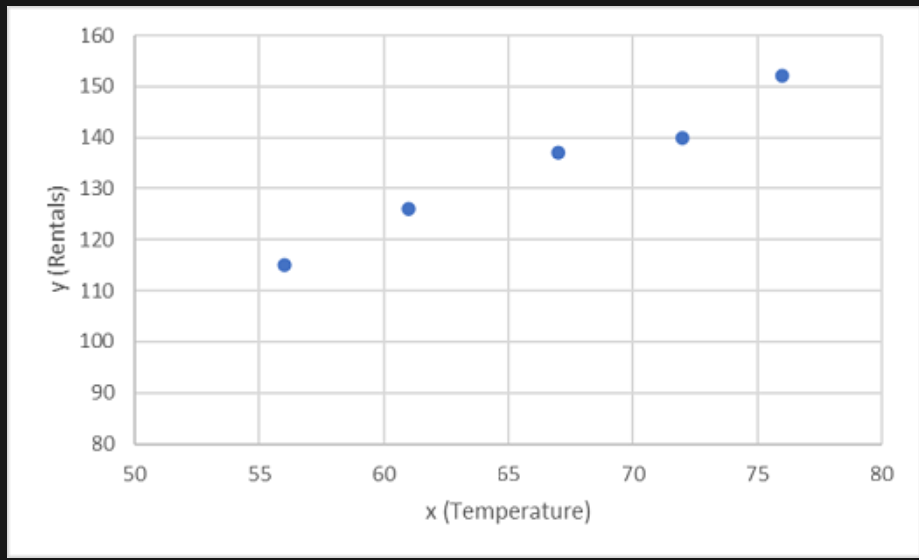
现在,需要将这些值拟合为一个函数,以实现一些随机变化。 你可能会发现绘制的点几乎形成了一条对角线,换句话说,x 和 y 之间存在明显的线性关系,因此我们需要找出最适合数据样本的线性函数。 可以使用多种算法来确定此函数,这些算法最终将找到一条与所绘制点的总体方差最小的直线,如下所示:
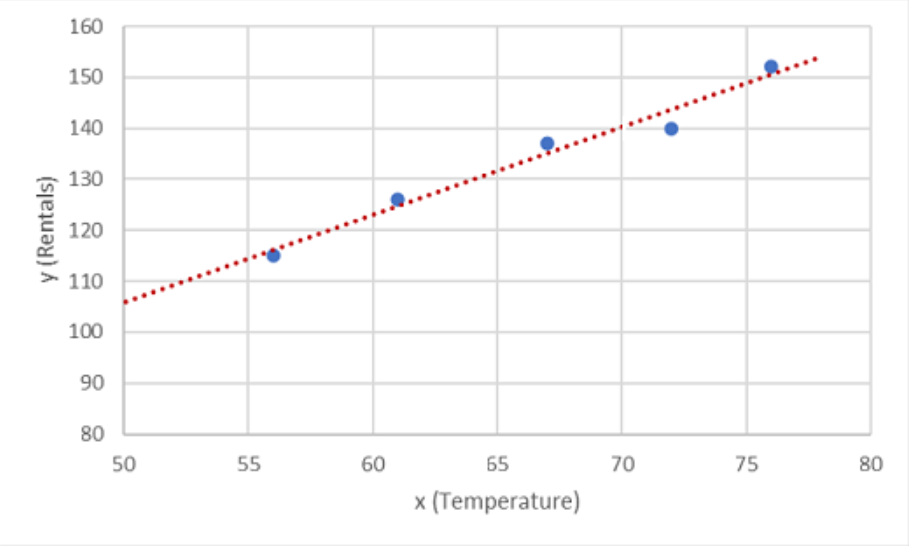
该线表示一个线性函数,可以将其与任何 x 值一起使用,以应用该线的斜率及其截距(当 x 为 0 时,该线与 y 轴交叉) 来计算 y。 在本例中,如果将该线向左延伸,会发现当 x 为 0 时 y 约为 20,并且该线的斜率决定了 x 每向右移动一个单位,y 会增加约 1.7。 因此,f 函数可以计算为 20 + 1.7 x。
现在我们已经定义了预测函数,可以使用它来预测所保留的验证数据的标签,并将预测值(通常用符号 ŷ 或“y-hat”表示) 与实际已知的 y 值进行比较。
| x | y | ŷ |
|---|---|---|
| 82 | 156 | 159.4 |
| 54 | 114 | 111.8 |
| 62 | 129 | 125.4 |
让我们看一下 y 和 ŷ 值在绘图中的比较情况:
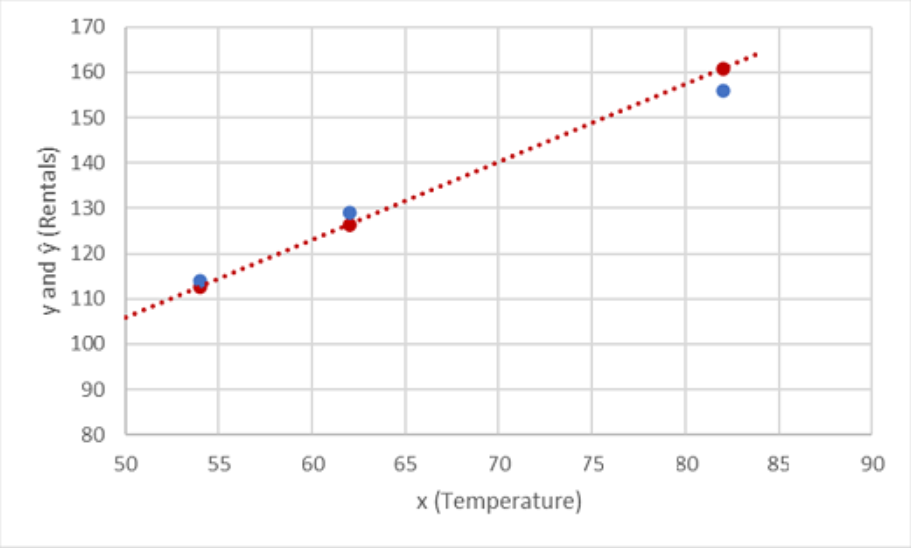
函数线上的绘制点是由函数计算的预测 ŷ 值,而其他绘制点是实际 y 值。
可以采用多种方法来度量预测值和实际值之间的差值,并且可以使用这些指标来评估模型的预测效果。
机器学习基于统计和数学,因此必须了解统计学家和数学家(以及数据科学家) 使用的特定术语。 可以将预测标签值与实际标签值之间的差值视为误差的度量。 但是实际上,“实际”值是基于样本观察值的(其本身可能会有一些随机变化) 。 要清楚,我们将预测值 (ŷ) 与观察值 (y) 进行比较,我们将它们之间的差值称为残差。 我们可以汇总所有验证数据预测的残差,以计算模型中的总体损失,作为对其预测性能的度量。
度量损失的最常见方法之一是对各个残差求平方,求平方和,然后计算平均值。 对残差进行平方处理可以使计算基于绝对值(忽略差值是负还是正) ,并对较大的差值赋予较大的权重 。此指标称为均方误差。
对于我们的验证数据,计算结果如下所示:
| y | ŷ | y - ŷ | (y - ŷ)2 |
|---|---|---|---|
| 156 | 159.4 | -3.4 | 11.56 |
| 114 | 111.8 | 2.2 | 4.84 |
| 129 | 125.4 | 3.6 | 12.96 |
| Sum | ∑ | 29.36 | |
| 平均值 | x̄ | _ 9.79* |
因此,基于 MSE 指标的模型损失为 9.79。
也就是说这个 MSE 应该指的就是均方误差
那有什么好处吗? 很难判断,因为 MSE 值未用有意义的度量单位表示。 我们知道,该值 越小,模型中的损失就越少,因此其预测效果越好。 这使它成为了比较两个模型并找到性能最好的模型的有用指标。
有时,用与预测标签值本身相同的度量单位来表示损失更为有用,在本例中,为租赁数。 为此,可以计算 MSE 的平方根,此操作必定会生成一个已知指标,即均方根误差 (RMSE)。
√9.79 = _3.13*
因此,模型的 RMSE 表明损失刚超过 3,可以粗略地解释为,平均而言,错误的预测约为 3 次租赁。
还有许多其他指标可用于度量回归中的损失。 例如,R2(R 平方) (有时称为确定系数) ,是 x 和 y 平方之间的相关性。 这会生成一个介于 0 和 1 之间的值,该值可测量模型可以解释的方差量。 通常,此值越接近 1,模型的预测效果就越好。
逻辑回归
部分内容为通篇摘抄, 含适当改动与注释
分类问题
监督学习的最主要类型
分类(Classification)
标签离散
- 身高1.85m,体重100kg的男人穿什么尺码的T恤?
- 根据肿瘤的体积、患者的年龄来判断良性或恶性?
- 根据用户的年龄、职业、存款数量来判断信用卡是否会违约?
输入变量可以是离散的,也可以是连续的
二分类
我们先从用蓝色圆形数据定义为类型1,其余数据为类型2;只需要分类1次
步骤:① ->②
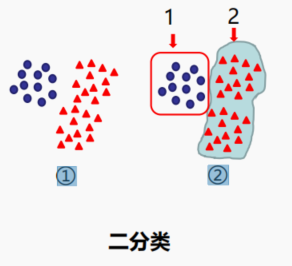
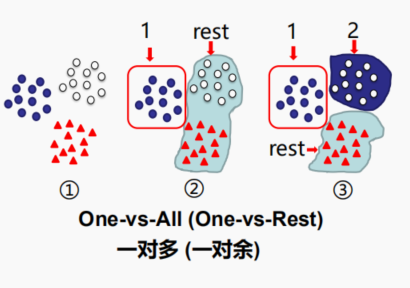
多分类
我们先定义其中一类为类型1(正类) ,其余数据为负类(rest) ;
接下来去掉类型1数据,剩余部分再次进行二分类,分成类型2和负类;
如果有𝑛类,那就需要分类 𝑛-1 次
步骤:① -> ② -> ③ -> ……
Sigmoid 函数
𝜎(𝑧) 代表一个常用的逻辑函数(logistic function) , 为𝑆形函数(Sigmoid function)
合起来,我们得到逻辑回归模型的假设函数:
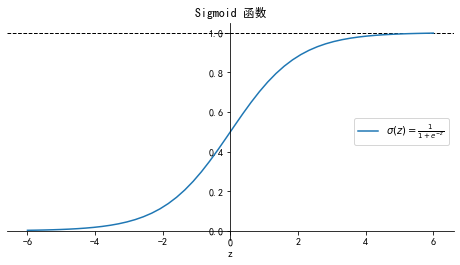
当 时, 预测
当 时, 预测
注意: 若表达式 $h(x) = z = w_0 + w_1 x_1 + w_2 x_2 + ... + w_n x_n + b $, 则 b 可以融入到 , 即:
线性回归的函数 , 范围是 。
而分类预测结果需要得到 的概率值。
在二分类模型中,事件的几率 odds:事件发生与事件不发生的概率之比为 , 称为事件的发生比(the odds of experiencing an event)
其中𝑝为随机事件发生的概率,𝑝的范围为 。
取对数得到: 而
求解得到:
将 𝑧 进行逻辑变换:
逻辑回归求解
假设一个二分类模型:
则:
逻辑回归模型的假设是:
其中 , 逻辑函数 (logistic function) 公式为:
损失函数
为了衡量算法在全部训练样本上的表现如何, 我们需要定义一个算法的代价函数, 算法的代价函数是对 m 个样本的损失函数求和然后除以 m:
代价函数
求解过程
似然函数为:
似然函数两边取对数, 则连乘号变成了连加号:
代价函数为:
统计学中,似然函数是一种关于统计模型参数的函数。给定输出x时,关于参数θ的似然函数L(θ|x)(在数值上) 等于给定参数θ后变量X的概率:L(θ|x)=P(X=x|θ)。
似然函数在推断统计学(Statistical inference) 中扮演重要角色,尤其是在参数估计方法中。在教科书中,似然常常被用作“概率”的同义词。但是在统计学中,二者有截然不同的用法。概率描述了已知参数时的随机变量的输出结果;似然则用来描述已知随机变量输出结果时,未知参数的可能取值。例如,对于“一枚正反对称的硬币上抛十次”这种事件,我们可以问硬币落地时十次都是正面向上的“概率”是多少;而对于“一枚硬币上抛十次”,我们则可以问,这枚硬币正反面对称的“似然”程度是多少。
逻辑回归代码实现
训练和评估分类模型
随笔基于 Microsoft Learn:训练和评估分类模型 - Learn | Microsoft Docs
部分内容为通篇摘抄, 含适当改动与注释
分类属于一种机器学习,用于将项目归入类中。
学习目标
- 何时使用分类
- 如何使用 Scikit-Learn 框架来训练和评估分类模型
简介
分类是一种机器学习形式,你在其中训练模型来预测某个项目属于哪个类别或类。 比如,一家健康诊所可能会使用患者身高、体重、血压和血糖水平等诊断数据来预测该患者是否患有糖尿病。
在该例子中,有两个可能的类(未患糖尿病和患有糖尿病) ,这使得该示例是一个二元分类。 通过以值的形式确定每个可能的类的概率来进行类预测,其中该值介于 0(不可能) 到 1(确信) 之间。 所有类的总概率为 1(患者肯定患者糖尿病或肯定未患糖尿病) ,因此如果预测出患者患有糖尿病的概率为 0.3,那么患者未患糖尿病的相应概率就是 0.7。 阈值通常为 0.5,它用于确定预测得到的类 - 如果正类(在本例中指患有糖尿病) 的预测概率大于阈值,那么预测分类为患有糖尿病。
还可创建多类分类模型,其中可能的类大于两个。 例如,这家健康诊所可能会扩充糖尿病模型,来将患者分类为未患糖尿病、含有 1 型糖尿病或患有 2 型糖尿病。 每个类概率值相加仍为 1(患者可能是这三类中的一种) ,模型会预测得出概率最大的类。
训练和评估分类模型
分类是一种有监督机器学习技术,这意味着它依赖已知特征值(例如患者的诊断测量值) 和已知标签值(例如分类为未患糖尿病或患有糖尿病) 等数据。 分类算法用于将数据的一部分拟合到函数中,该函数可根据特征值计算每个类标签的概率。 剩余数据用于将它根据特征生成的预测与已知类标签进行比较来评估模型。
一个简单示例
我们来看一个简单的示例,它可帮助阐释关键原则。 假设我们有以下患者数据,其中包含一个特征(血糖水平) 和一个类标签(0 表示未患糖尿病,1 表示患有糖尿病) 。
| 血糖 | 糖尿病 |
|---|---|
| 82 | 0 |
| 92 | 0 |
| 112 | 1 |
| 102 | 0 |
| 115 | 1 |
| 107 | 1 |
| 87 | 0 |
| 120 | 1 |
| 83 | 0 |
| 119 | 1 |
| 104 | 1 |
| 105 | 0 |
| 86 | 0 |
| 109 | 1 |
我们将使用观察到的前 8 个值来训练分类模型,我们将先绘制出血糖特征(将其命名为 x) 和预测的糖尿病标签(将其命名为 y) 。

我们需要一个函数,用它来根据 x 计算 y 的概率值(换句话说,我们需要函数 f(x) = y) 。 从图表中可以看到,血糖水平低的患者全都未患糖尿病,而血糖水平更高的患者患有糖尿病。 似乎血糖水平越高,患者患有糖尿病的概率就越大,拐点在 100 到 110 之间的某个位置。 我们需要拟合一个函数,计算 y 轴介于 0 到 1 的某个值来得到这些值。
logistic 函数就是这样的一个函数,它得出 S 形曲线,如下所示:

Logistic函数或Logistic曲线是一种常见的S形函数,它是皮埃尔·弗朗索瓦·韦吕勒在1844或1845年在研究它与人口增长的关系时命名的。广义Logistic曲线可以模仿一些情况人口增长(P) 的S形曲线。起初阶段大致是指数增长;然后随着开始变得饱和,增加变慢;最后,达到成熟时增加停止。
现在,我们可使用该函数,查找 x 的函数行上的点来根据 x 的任意值计算 y 为阳性(即患者患有糖尿病) 的概率值;我们可设置阈值 0.5 作为类标签预测的分界点。 让我们用保留的数据值测试一下。

在阈值线下方绘制的点将生成预测类 0(未患糖尿病) ,在该线上方的点将被预测为 1(患有糖尿病) 。
现在,我们可根据模型中封装的 logistic 函数,将标签预测结果(ŷ,也写做“y-hat”)与实际的类标签 (y) 进行比较。
| x | y | ŷ |
|---|---|---|
| 83 | 0 | 0 |
| 119 | 1 | 1 |
| 104 | 1 | 0 |
| 105 | 0 | 1 |
| 86 | 0 | 0 |
| 109 | 1 | 1 |
我们可对结果制表形成一个名为“混淆矩阵”的结构,如下所示:

该混淆矩阵显示了所有用例的总数,其中:
- 模型预测得到 0,且实际标签为 0(真阴性)
- 模型预测得到 1,且实际标签为 1(真阳性)
- 模型预测得到 0,而实际标签为 1(假阴性)
- 模型预测得到 1,而实际标签为 0(假阳性)
混淆矩阵中的单元格通常带有阴影;值越大,阴影越重。 这样,可更轻松地按从左上角到右下角的顺序看到强烈的对角线趋势,突出显示预测值和实际值相同的单元格。
通过这些核心值,你可对一些其他指标进行计算,这可帮助你评估模型的性能。 例如:
- 准确度:(TP+TN)/(TP+TN+FP+FN) - 也就是说在所有预测中,有多少是正确的?
- 召回率:TP/(TP+FN) - 也就是说在所有为阳性的用例中,模型识别出了其中的多少个?
- 精准率:TP/(TP+FP) - 换句话说在模型预测为阳性的所有用例中,实际上有多少是阳性的?
- TP:被模型预测为正类的正样本
- TN:被模型预测为负类的负样本
- FP:被模型预测为正类的负样本
- FN:被模型预测为负类的正样本
True, False, Positive, Negative
Exercise - Train and evaluate a classification model
无监督学习
- 区别于监督学习,无监督学习希望机器做到无师自通,在完全没有任何标签的情况下,机器到底能学到什么样的知识 如:通过多维度的用户行为分析,广告投放 推荐系统 异常查找
无监督学习基本算法 -- 聚类分析 K-means
- 是在没有给定划分类别的情况下,根据数据的相似度进行分组的一种方法,分组的原则是组内距离最小化而组间距离最大化;
- K-means 算法是典型的基于距离的非层次聚类算法,在最小化误差函数的基础上将数据划分为预定的K类别,采用距离作为相似性的评级指标,即认为两个对象的距离越近,其相似度越大。
- 1、随机设置K个特征空间内的点作为初始的聚类中心
- 2、对于其他每个点计算到K个中心的距离,未知的点选择最近的一个聚类中心点作为标记类别
- 3、接着对着标记的聚类中心之后,重新计算出每个聚类的新中心点(平均值)
- 4、如果计算得出的新中心点与原中心点-样,那么结束,否则重新进行第二步过程
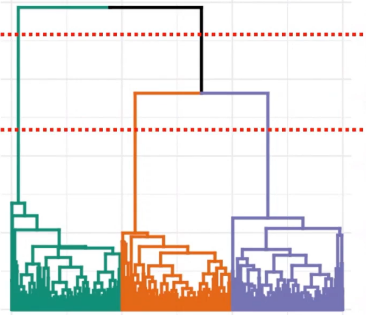
无监督学习基本算法 -- 聚类分析 Hierarchical Clustering
- 分层聚类通过分割方法或聚集方法创建聚类。除法是一种"自上而下”的方法,从整个数据集开始,然后逐步查找分区。凝聚聚类是一种"自下而上”的方法。
- (1)初始化:把每个样本各自归为一类(每个样本自成一 类)计算每两个类之间的距离,在这里也就是样本与样本之间的相似度(本质还是计算类与类之间的距离)。
- (2)寻找各个类之间最近的两个类,把它们归为一类(这样类的总数就减少了一个)
- (3)重新计算新生成的这个类与各个旧类之间的距离(相似度)
- (4)重复(2) (3) 步,直到所有的样本都归为一类, 结束。
6.神经网络
6.1神经网络介绍
6.1.1 前馈神经网络
前馈神经网络(Feed Forward Neural Network) 是一种单向多层的网络结构,即信息是从输入层开始,逐层向一个方向传递,一直到输出层结束。所 谓 的 “前馈”是指输入信号的传播方向为前向, 在此过程中并不调整各层的权值参数,而反传播时是将误差逐层向后传递,从而实现使用权值参数对特征的记忆,即通过反向传播(BP) 算法来计算各层网络中神经元之间边的权重。BP算法具有非线性映射能力,理论上可逼近任意连续函数,从而实现对模型的学习
由于前馈神经网络使用 BP 算法, 所以有时也将其称为 BP 神经网络